问题
填空题
设函数f(x)连续，f(0)=1，令
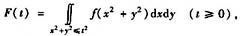则F"(0)=______。
答案
参考答案：2π
解析：
[分析]： 从被积函数f(x2+y2)及积分域x2+y2≤t2看，显然取极坐标变换，变成变上限的定积分后可对上限的变量求导，因题目中只给出f(x)连续，所以F"(0)要由定义来计算。
作极坐标变换，令x=rcosθ，y=rsinθ，则
[*]
因为f(x)连续，所以F’(t)=2πtf(t2)，且F’(0)=0，于是
[*]
[*]