问题
问答题
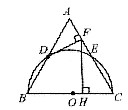
如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、E,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H.若等边△ABC的边长为4,求FH的长.(结果保留根号)
答案
参考答案:
(1)DF与⊙O相切.连接OD,
∵△ABC是等边三角形,DF⊥AC,
∴∠ADF=30°.
∵OB=OD,∠DB0=60°,
∴∠BDO=60°.
∴∠ODF=180°-∠BD0-∠ADF=90°.
∴DF是⊙O的切线.
(2)∵AD=BD=2,ADF=30°,∴AF=1.
∴FC=AC-AF=3.
∵FH⊥BC,
∴∠FHC=90°
在Rt△FHC中,
sin∠FCH= FH /FC ,
∴FH=FC•sin60°= 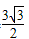 .
.
即FH的长为 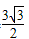 .
.
