问题
问答题
设曲线
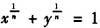 (正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n),证明:
(正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n),证明:
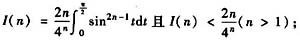
答案
参考答案:对题(Ⅰ)中的I(n)表达式,令t=sinθ,则有
[*] ①
方法1。 将①式作如下变形
[*]
方法2。 将①式作如下变形
[*] ②
将①,②两式相加得
[*]
由连续函数定积分的比较性质可得[*],从而
[*] ③
设曲线
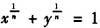 (正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n),证明:
(正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n),证明:
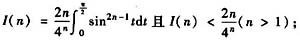
参考答案:对题(Ⅰ)中的I(n)表达式,令t=sinθ,则有
[*] ①
方法1。 将①式作如下变形
[*]
方法2。 将①式作如下变形
[*] ②
将①,②两式相加得
[*]
由连续函数定积分的比较性质可得[*],从而
[*] ③