问题
问答题
求幂级数
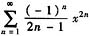的收敛半径，收敛域与和函数。
答案
参考答案：因幂级数[*]中所有x2n-1项的系数都是零，所以直接利用比值判别法求其收敛半径，当x=0时幂级数显然收敛，设x≠0，因
[*]
可见幂级数[*]当|x|＜1时绝对收敛，当|x|＞1时发散，故幂级数的收敛半径R=1。
当x=±1时幂级数成为交错级数[*]由于[*]单调减少且[*]按莱布尼兹判别法可知幂级数在x=-1与x=1都收敛，即其收敛域为[-1，1]。
设[*]则幂级数[*]当-1＜x＜1时由于
[*]
利用S1(0)=0，积分可得S1(x)=-arctanx，从而当|x|＜1时
[*]
由于上式左端的幂级数在x=-1与x=1收敛，而函数-xarctanx在x=-1与x=1都连续，故当-1≤x≤1时有
[*]