问题
问答题
设曲线
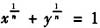(正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n)，证明：
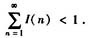
答案
参考答案：由[*]及③式可知
[*]
由比值判别法易知正项级数[*]收敛，为求其和，先求其前n项的部分和
[*]
又[*]
由④式减去⑤式即得
[*]
[*]从而有
[*]
故[*]进而就有[*]
搜题请搜索小程序“爱下问搜题”
设曲线
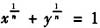(正整数n≥1)在第一象限与坐标轴围成图形的面积为I(n)，证明：
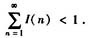
参考答案：由[*]及③式可知
[*]
由比值判别法易知正项级数[*]收敛，为求其和，先求其前n项的部分和
[*]
又[*]
由④式减去⑤式即得
[*]
[*]从而有
[*]
故[*]进而就有[*]
、
、
、
、