问题
填空题
对正整数n,设曲线y=xn(1-x)在x=2处的切线与y轴交点的纵坐标为an,则数列
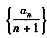 的前n项和的公式是()。
的前n项和的公式是()。
答案
参考答案:2n+1-2
解析:
由题意知当x=2时,y=-2n,即切点坐标为(2,-2n),又有y’|x=2=n·2n-1-(n+1)·2n,则切线方程可表示为y+2n=[n·2n-1-(n+1)·2n](x-2),又当x=0时,有y=an,则[*]
对正整数n,设曲线y=xn(1-x)在x=2处的切线与y轴交点的纵坐标为an,则数列
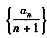 的前n项和的公式是()。
的前n项和的公式是()。
参考答案:2n+1-2
解析:
由题意知当x=2时,y=-2n,即切点坐标为(2,-2n),又有y’|x=2=n·2n-1-(n+1)·2n,则切线方程可表示为y+2n=[n·2n-1-(n+1)·2n](x-2),又当x=0时,有y=an,则[*]