问题
计算题
如图所示，一水平直轨道CF与半径为R的半圆轨道ABC在C点平滑连接，AC在竖直方向，B点与圆心等高。一轻弹簧左端固定在F处，右端与一个可视为质点的质量为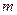
的小铁块甲相连。开始时，弹簧为原长，甲静止于D点。现将另一与甲完全相同的小铁块乙从圆轨道上B点由静止释放，到达D点与甲碰撞，并立即一起向左运动但不粘连，它们到达E点后再返回，结果乙恰回到C点。已知CD长为L1，DE长为L2，EC段均匀粗糙，ABC段和EF段均光滑，弹簧始终处于弹性限度内。
（1）求直轨道EC段与物块间动摩擦因素.
（2）要使乙返回时能通过最高点A，可在乙由C向D运动过程中过C点时，对乙
加一水平向左恒力，至D点与甲碰撞前瞬间撤去此恒力，则该恒力至少多大？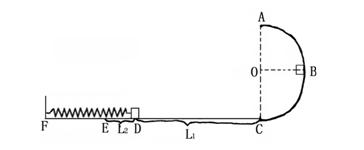
答案
（1）设乙与甲碰前瞬间速度为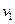
，碰后瞬间速度为
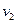，甲乙一起返回到D时速度为
.
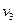乙从B到D有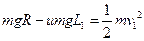 
①-------（2分）
碰撞过程由动量守恒得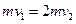 
②-------（2分）
甲乙从D到E再回到D有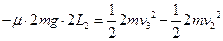 
③--（3分）
乙从D到C 有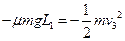 
④-------（3分）
联立解得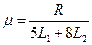
（2）设对乙加的最小恒力为F
从B到D有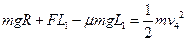 
⑤-------（2分）
碰撞过程由动量守恒得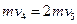 
⑥---（1分）
甲乙从D到E再回到D有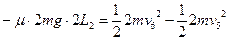
⑦-（1分）
乙从D到A有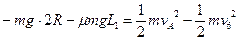
⑧-------（2分）
在A点有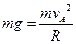 
⑨-------（2分）
联立⑤⑥⑦⑧⑨解得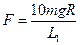
--------------------（2分）