问题
单项选择题
设f(x)在[a，b]上可导，且f’(a)f’(b)＜0，则下列命题
①至少存在一点x0∈(a，b)，使得f(x0)＜f(a)
②至少存在一点x0∈(a，b)，使得f(x0)＞f(b)
③至少存在一点x0∈(a，b)，使得f’(x0)=0
④至少存在一点x0∈(a，b)，使得f(x0)=
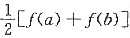
正确的个数为______
A．1．
B．2．
C．3．
D．4．
答案
参考答案：A
解析： 因为f’(a)f’(b)＜0，不妨设f’(a)＜0，f’(b)＞0，
则
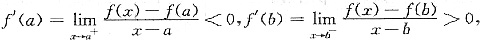
由极限的保号性可得，存在x1，x2∈(a，b)，使得
f(x1)-f(a)＜0，f(x2)-f(b)＜0，
所以f(a)，f(b)不是f(x)在[a，b]上的最小值，所以f(x)在[a，b]上的最小值只可能在(a，b)内取得，由费尔马定理可知，至少存在一点x0∈(a，b)，使得f’(x0)=0．
其他命题可用举反例排除法来求解．
令f(x)=x-x2，则f(x)在[0，1]可导，且
f’(0)=1，f’(1)=-1
f’(0)f’(1)=-1＜0．
但对于x∈(0，1)，f(x)=x(1-x)＞0=f(0)=f(1)，可排除①④；
令f(x)=x2-x，则f(x)在[0，1]可导，且
f(0)=-1，f’(1)=1
f’(0)f’(1)=-1＜0，
但对于x∈(0，1)，f(x)=x(x-1)＜0=f(0)=f(1)，可排除②．
综上，故选A．