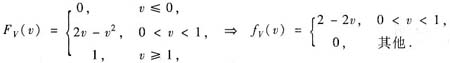问题
问答题
设随机变量X与Y相互独立,且都在[0,1]上服从均匀分布,试求:
1.U=XY的概率密度fU(u);
答案
参考答案:方法1° 分布函数法.由题设知
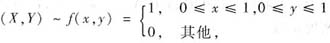
所以V=|X-Y|的分布函数FV(v)=P{|X-Y|≤v}.
当v≤0时,FV(v)=0;当v>0时,
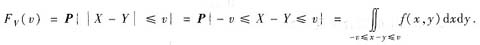
由图形知,当v≥1时,FV(v)=1;当0<v<1时,
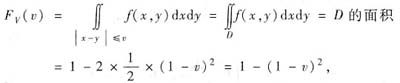
其中D={(x,y):0≤x≤1,0≤y≤1,|x-y|≤v}.
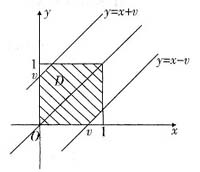
综上得

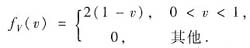
方法2° 公式法.记Z=X-Y=X+(-Y),其中X与(-Y)独立,概率密度分别为
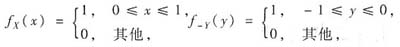
由卷积公式得Z的概率密度
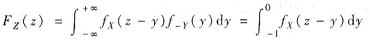
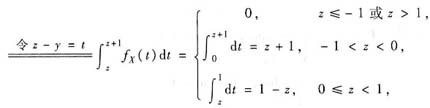
V=|X-Y|=|Z|的分布函数为FY(v)=P{|Z|≤v},
当v≤0时,FV(v)=0;当v>0时,
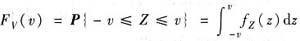 ;
;
由此知,当0<v<1时,
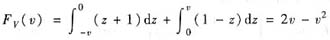 ;
;
当v≥1时,
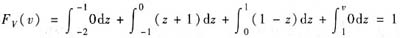 .
.
综上得