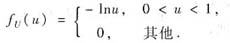问题
问答题
设随机变量X与Y相互独立,且都在[0,1]上服从均匀分布,试求:
1.U=XY的概率密度fU(u);
答案
参考答案:由于X与Y相互独立且密度函数已知,因此我们可以用两种方法:分布函数法与公式法求出U、V的概率密度.
方法1° 分布函数法.由题设知(X,Y)联合概率密度
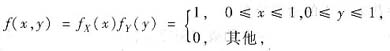
所以U=XY的分布函数
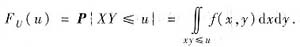
当u≤0时,FU(u)=0;当u≥1时,FU(u)=1;当0<u<1时,
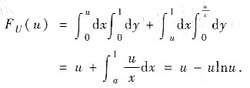
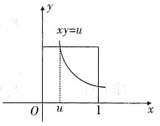
综上得
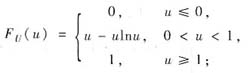
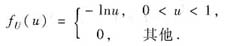
方法2° 公式法.已知
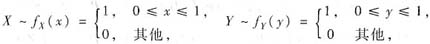 X与Y独立,由独立乘积概率密度公式得
X与Y独立,由独立乘积概率密度公式得
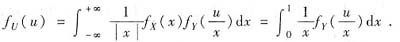
由fY(y)表达式知,
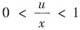 ,即0<u<x<1时,
,即0<u<x<1时,
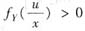 ,否则
,否则
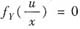 ,故当0<u<1时,令
,故当0<u<1时,令
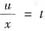 ,则
,则
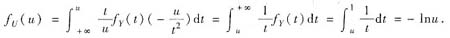
所以