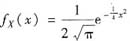问题
问答题
已知随机变量X1，X2，X3，X4相互独立，X1与X2服从标准正态分布，X3、X4为离散型随机变量且有相同的概率分布：
，试求X=X1X3-X2X4的概率密度函数fX(x)．
答案
参考答案：记Y1=X1X3，Y2=X2X4，依题设知Y1与Y2独立且有相同的分布，即
F(y)=P{Y1≤y}=P{X1X3≤y}
=P{X1X3≤y，X3=-1}+P=X1X3≤y，X3=1}
=P{-X1≤y，X3=-1}+P{X1≤y，X3=1}
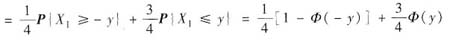
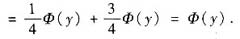
所以Yi～N(0，1)(i=1，2)且相互独立，X=Y1-Y2～N(0，2)，X的概率密度
