问题
问答题
已知随机变量X，Y的概率分布分别为P
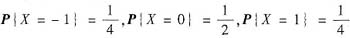；PY=0=
，并且PX+Y=1=1，求：(Ⅰ)(X，Y)的联合分布；(Ⅱ)X与Y是否独立是否相关为什么．
答案
参考答案：首先由边缘分布及条件求得联合分布，进而判断是否独立，是否相关．
(Ⅰ)由题设P{X+Y=1}=1，即P{X=-1，Y=2}+P{X=0，Y=1}+P{X=1，Y=0}=1，故其余分布值均为零，即P{X=-1，Y=0}=P{X=-1，Y=1}=P{X=0，Y=0}=P{X=0，Y=2}=P{X=1，Y=1}=P{X=1，Y=2}=0，由此可求得联合分布
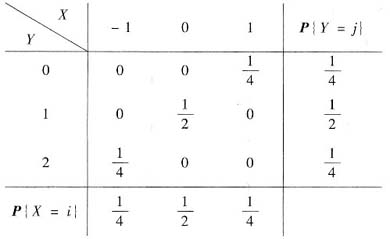
(Ⅱ)因为P{X=-1，Y=0}=0≠P{X=-1}P{Y=0}=
，故X与Y不独立，又EX=0，P{XY=-2}=
，
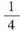≠0=EXEY，故X与Y相关．(由此知X与Y不独立．)