问题
问答题
带权图(权值非负，表示边连接的两顶点间的距离)的最短路径问题是找出从初始顶点到目标顶点之间的一条最短路径。假定从初始顶点到目标顶点之间存在路径，现有一种解决该问题的方法：
①设最短路径初始时仅包含初始顶点，令当前顶点u为初始顶点；
②选择离u最近且尚未在最短路径中的一个顶点v，加入到最短路径中，修改当前顶点u=v：
③重复步骤②，直到u是目标顶点时为止。
请问上述方法能否求得最短路径若该方法可行，请证明之；否则，请举例说明。
答案
参考答案：贪心算法：
每次只选择离u最近且尚未在最短路径中的一个顶点v，加入到最短路径中。
贪心算法并不一定能够得到最优解；
例如，对于下列所示的带权图，如果按照题中的原则，从A到C的最短路径是A→B→C，事实上其最短路径是A→D→C。
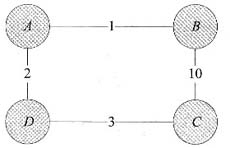
因此，利用该方法求得不一定是最短路径。