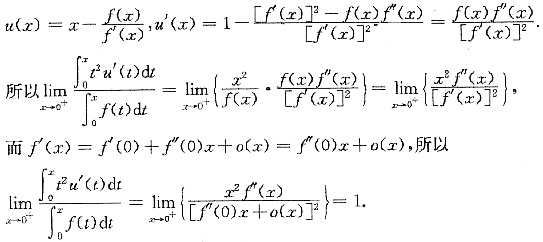问题
问答题
设f’’(x)连续且f’’(x)＞0，f’(0)=0，求极限
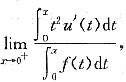其中u(x)是曲线y=f(x)在x点处的切线在z轴上的截距．
答案
参考答案：
解析：
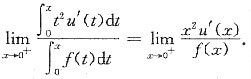
由导数的几何意义，曲线y=f(x)在x点处的切线方程为
Y-f(x)=f’(x)(X-x)，
令Y=0，则
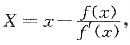于是
搜题请搜索小程序“爱下问搜题”
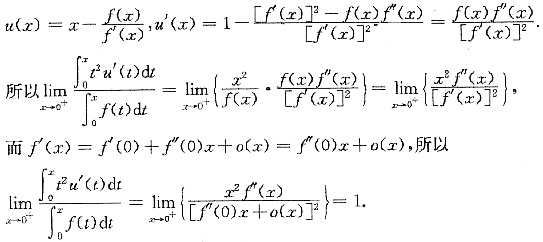
设f’’(x)连续且f’’(x)＞0，f’(0)=0，求极限
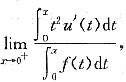其中u(x)是曲线y=f(x)在x点处的切线在z轴上的截距．
参考答案：
解析：
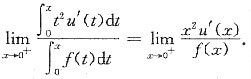
由导数的几何意义，曲线y=f(x)在x点处的切线方程为
Y-f(x)=f’(x)(X-x)，
令Y=0，则
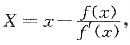于是