问题
问答题
将边长为2a的正方形纸板的四角各剪去一个边长相等的小正方形,然后将其做成一个无盖的纸盒.问剪去的小正方形边长为多少时,纸盒容积最大?
答案
参考答案:
设剪去的小正方形边长为z(0<x<a),则折起纸盒容积为V=4(a-x)2x.
令V′=4(a-x)(a-3x)=0,
得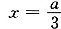 ,或x=a(不合题意,舍去).
,或x=a(不合题意,舍去).
而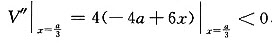
所以,当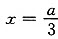 时,V有极大值,也是最大值,即剪去的小正方形边长为
时,V有极大值,也是最大值,即剪去的小正方形边长为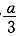 .
.
将边长为2a的正方形纸板的四角各剪去一个边长相等的小正方形,然后将其做成一个无盖的纸盒.问剪去的小正方形边长为多少时,纸盒容积最大?
参考答案:
设剪去的小正方形边长为z(0<x<a),则折起纸盒容积为V=4(a-x)2x.
令V′=4(a-x)(a-3x)=0,
得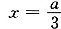 ,或x=a(不合题意,舍去).
,或x=a(不合题意,舍去).
而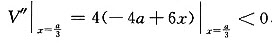
所以,当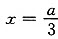 时,V有极大值,也是最大值,即剪去的小正方形边长为
时,V有极大值,也是最大值,即剪去的小正方形边长为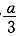 .
.