问题
填空题
曲线y=lnx上与直线x+y=1垂直的切线方程为（）。
答案
参考答案：x-y-1=0
解析：
设过曲线y=lnx上一点(x0，y0)的切线与直线x+y=1垂直，可知切线斜率k=1.
由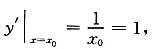
得x0=1，y0=ln1=0．
故所求切线为
y-0=x-1，
即x-y-1=0．
搜题请搜索小程序“爱下问搜题”
曲线y=lnx上与直线x+y=1垂直的切线方程为（）。
参考答案：x-y-1=0
解析：
设过曲线y=lnx上一点(x0，y0)的切线与直线x+y=1垂直，可知切线斜率k=1.
由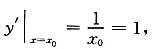
得x0=1，y0=ln1=0．
故所求切线为
y-0=x-1，
即x-y-1=0．