问题
问答题
设某产品的成本函数为C=aq2+bq+c，需求函数为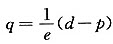
，其中c为成本，g为需求量(即产量)，p为单价；a，b，f，d，e均为正常数，且d＞b，求：
(1)利润最大时的产量和最大利润；
(2)需求对价格的弹性；
(3)需求对价格弹性的绝对值为1时的产量．
答案
参考答案：
(1)利润L为收入减去成本，即
L=pq-C
=(d-eq)q-(aq2+bq+c)
=-(e+a)q2+(d-b)q-c．
令L′(q)=-2(e+a)q+(d-b)=0，得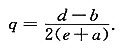
因为L″(q)=-2(e+a)＜0，所以，当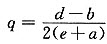
时，利润最大，最大利润为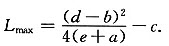
(2)根据弹性的定义，需求对价格的弹性
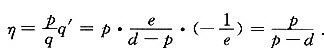
(3)由|η|=1，得