问题
填空题
设函数y=f（x）由方程x+2lnx=y4所确定，则曲线y=f（x）在点（1，1）处的切线方程是（）。
答案
参考答案：x-y=0
解析：
点(1，1)在曲线y=f(x)上，在已知方程两边对x求导，得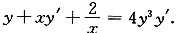
由上式可得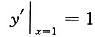
，故所求切线方程为
y-1=x-1，
即x-y=0．
搜题请搜索小程序“爱下问搜题”
设函数y=f（x）由方程x+2lnx=y4所确定，则曲线y=f（x）在点（1，1）处的切线方程是（）。
参考答案：x-y=0
解析：
点(1，1)在曲线y=f(x)上，在已知方程两边对x求导，得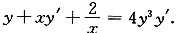
由上式可得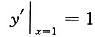，故所求切线方程为
y-1=x-1，
即x-y=0．