问题
问答题
设X1，X2，…，Xn+m(n＞m)独立同分布，且有有限期望与方差．
试求：
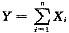与
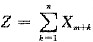的相关系数．
答案
参考答案：[详解] 设E(Xk)=a，D(Xk)=σ2，则
cov(Y，Z)=E[(Y-EY)(Z-EZ)]
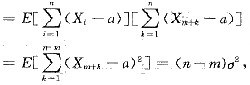
又DY=DZ=nσ2，所以
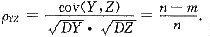
解析：
[分析]： 利用期望、方差及协方差的运算性质进行计算即可．
[评注] 数字特征的计算一般通过分布利用定义进行讨论．但对于抽象的随机变量，应注意利用运算性质进行推理．本题中，[*]
=E{[(X1-a)+…+(Xm-a)+(Xm+1-a)+…+(Xn-a)]
[(Xm+1-a)+…+(xn-a)+(Xn+1-a)+…+(Xn+k-a)]}应注意(X1-a)+…+(Xm-a)与(Xm+1-a)+…+(Xn-a)以及(Xn-1-a)+…+(Xn+k-a)相互独立，再利用相互独立随机变量积的数学期望等于数学期望的积，这样可方便地化简．