问题
问答题
设函数满足条件|f(x)-f(y)|≤k|x-y|，x，y∈[a，b]，0＜k＜1．取x0∈[a，b]，构造序列fn(x0))：f1(x0)=f(x0)，…，fn+1(x0)=f[fn(x0)]，n=1，2，…．
证明：(1)
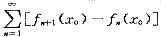绝对收敛；
(2)
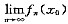存在．
答案
参考答案：[详解] (1)由已知，有
|fn+1(x0)-fn(x0)|=f[fn(x0)]-f[fn-1(x0)]|≤k|fn(x0)-fn-1(x0)|≤…≤kn-1|f[f(x0)]-f(x0)|≤kn|f(x0)-x0|．
∵当0＜k＜1时，
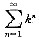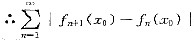收敛，
收敛，
即
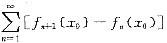绝对收敛．
(2)Sn=[f2(x0)-f1(x0)]+[f3(x0)-f2(x0)]+…+[fn+1(x0)-fn(x0)]
=fn+1(x0)-f1(x0)，
由(1)知
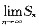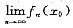存在，∴
存在．
解析：
[分析]： 由已知条件可得|fn+1(x0)-fn(x0)|≤kn|f(x0)-x0|．
[评注] [*]