问题
问答题
设z=f(x,y)在点(1，1)处可微，且f(1,1)=1，
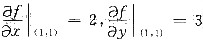，ψ(x)=f(x，f(x，x))，求
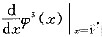
答案
参考答案：[详解] ψ(1)=f(1，f(1，1))=f(1，1)=1．
ψ’(x)=f’1(x，f(x，x))+f’2(x，f(x，x))[f’1(x，x)+f’2(x，x)]
∴ψ’(1)=f’1(1，f(1，1))+f’2(1，f(1，1))[f’2(1，1)+f’2(1，1)]
=f’1(1，1)+f’2(1，1)[f’1(1，1)+f’2(1，1)]
=2+3(2+3)=2+15=17．
[*]
解析：
[分析]： 记f’x=f’1，f’y=f’2，所以已知条件为f’1(1，1)=2，f’2(1，1)=3．
[评注] 求ψ’(x)时应注意复合的步骤，不要遗漏．