问题
问答题
设r
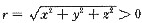，函数u=f(r)在0＜r＜+∞内具有连续的一阶导数，且在r＞0的小邻域内f(r)有界，又设f(r)满足div gradf(r)=lnr，求f(r)．
答案
参考答案：[详解]
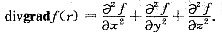
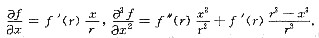
类似可计算另两个偏导数
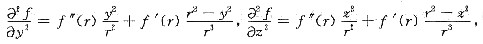
于是原方程化为
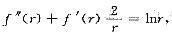
改写为 r2f"(r)+2rf’(r)=r2lnr，即(r2f’(r))’=r2lnr．
所以
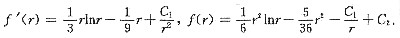
由条件f(r)在r＞0的小邻域内有界，所以应该C1=0．
故
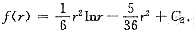
解析：
[分析]： 根据div(gradf(r))=[*]知，只需求出[*]，再由已知关系式转化为微分方程，然后再解此方程即可．
[评注] 微分方程[*]也可令f’(r)=u，转化为一阶线性微分方程[*]=lnr，再用标准公式求通解即可．