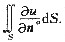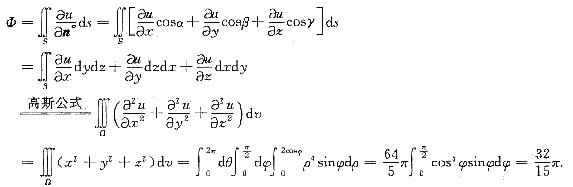阅渎下面的文字,完成1一3题。
大约50年前,知识分子和批评家们才开始忙于构建或重构有关何种文化有利于我们、何种文化是糟糕的文化的等级划分理论。美国丈人多维特。麦克唐纳曾写了一篇题为《大众文化和中产文化》的著名文章。他提出,大众文化和中产文化其实都是传统高雅文化退化后的产物。美国著名艺术批评家克莱门特·格林伯格在一篇有广泛影响力的关于现代油画的文章中对“先锋艺术”和“庸俗艺术”作了一番考察,他非常支持先锋艺术,认为它是人类精神所必不可少的,同时,他将后者谴责为法西斯运动的导火线。但从笔者与一批继承了麦克唐纳和格林伯格观点的文人和知识分子的交谈中发现,如今我们生活在一个等级层次阙如、近乎乌托邦的文化世界中。我所认识的大多数人都与我一样拥有反差极大的口味爱好:一边在看《南方公园》(美国的一部喜剧动画剧集),一边欣赏着舒伯特的音乐;既能沉浸在詹姆斯·凯恩(美国硬派小说代表作家)情节紧凑的小说中,也喜欢安东尼奥带有哲学探索意味的艺术电影。
资深旅游作家皮科·耶尔告诉笔者:“近几个夏天里最值得一提的事就是观看喜剧电影《疯狂神父》。”和其他正规的21世纪新人一样,耶尔的爱好也是混杂的:今年夏天,他最喜欢的电影是《四月三周又两天》,一部主题沉重的罗马尼亚艺术片。“对我来说,什么高雅和低俗、罪愆和无辜、大众文化和中产文化都已经过时了,正如东方西方、新旧这些观念一样。”耶尔说道。他认为全球化和互联网已对所有的东西进行了重新洗牌。“如今的那些最富吸引力的艺术家,从萨尔曼·拉什迪(著名的印度裔英国作家)到冰岛摇滚乐队SigurRos,无不在以各种方式混淆着文化阶层的界限,以至于我们乐得不知道究竟我们是得到了艺术的升华还是得到了娱乐。”
但文化阶层的这一融合怎么会发生得如此迅速而彻底?
小说家兼影评家斯蒂夫·埃里克森认为:“与其他东西一样,大众传媒打破了高雅文化与通俗文化之间的界线。”他说:“‘披头士’之所以风靡世界,一个原因在于他们出现在了时间轴的一个恰当的点上。”出道时的他们可以上电视节目露面,又能登上杂志封面,还能录制唱片,让全世界以前所未有的快捷速度听到他们的歌曲。由于“披头士”对古典音乐和实验音乐都有兴趣,他们使得高雅、低俗间的严格区分不再有效。光是凭着1966年的《左轮手枪》专辑,埃里克森说:“披头士就抹去了所有这些层次之分。”
其他方面的界线也在日益消融。曾经不受欢迎的音乐家,如去年夏天去世的迷幻牛仔李·海泽伍德(老牌乡村音乐歌手、作曲家),如今变得非常“酷”,“因为人们重新开始不带文化偏见地用崭新的耳朵去倾听他的音乐。”埃里克森说道,“如今的孩子们可以直接到YouTube网站观看他们要看的东西,而无需背负传统的包袱。
但有时候,我在想我们是不是太急于抹杀文化层次之间的差别了。我一直有种担忧,随着我们失去了分辨真正品质的能力,我们得到的只是低质产品。(选自《正在消失的文化分界》)
1.下列各项表述,不符合文意的两项是( )
A.美国著名艺术批评家克莱门特·格林伯格所说的“先锋艺术”和“庸俗艺术”即本文所说的高雅文化与通俗文化,克莱门特·格林伯格支持高雅文化。
B.作者与一批继承了麦克唐纳和格林伯格观点的文人和知识分子一样,都认为如今我们生活在一个没有尊贵卑贱等级层次、近乎乌托邦的世界中。
C.安东尼奥的艺术电影属于高雅文化,美国作家詹姆斯·凯恩情节紧凑的小说属于通俗文化。
D.罗马尼亚艺术片《四月三周又两天》属于高雅文化,喜剧电影《疯狂神父》属于通俗文化。
E.“披头士”的《左轮手枪》专辑属于高雅文化,冰岛摇滚乐队SigurRos属于通俗文化。
2.文化分界消失的原因是什么?
____________________________________________________________
3.对文化分界的消失,作者持怎样的态度?
____________________________________________________________
 .n°为S的外法线方向的单位向量.
.n°为S的外法线方向的单位向量.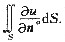
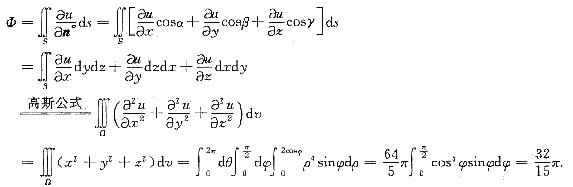
 .n°为S的外法线方向的单位向量.
.n°为S的外法线方向的单位向量.