问题
问答题
设随机变量X、Y相互独立，且
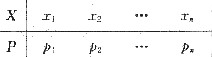．f(y)是Y的概率密度，令U=X+U，求U的概率密度．
答案
参考答案：[详解] 设U的分布函数为FU(u)，则
FU(u)=P(U≤u)=P(X+Y≤u)
=P(X+Y≤u|X=x1)P(X=x1)+P(X+Y≤u|X=x2)P(X=x2)+…+P(X+Y≤u|X=xn)P(X=xn)
=P(x1+Y≤u)P(X=x1)+P(x2+Y≤u)P(X=x2)+…+P(xn+Y≤u)P(X=xn)
=P(Y≤u-x1)p1+P(Y≤u-x2)p2+…+P(Y≤u-xn)pn
=FY(u-x1)p1+FY(u-x2)p2+…+FY(u-xn)pn
∴fU(u)={FU(u))’=f(u-x1)p1+f(u-x2)pz+…+f(u-xn)pn
=
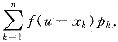
解析：
[分析]： U为离散型和连续型随机变量的和．解这类问题的关键是全概公式．
[评注] 对二维随机变量的各种问题，经常使用全概公式，应熟练掌握求解该题的方法．
vBl
vBl