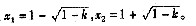问题
问答题
设函数,f(x)=ax2+bx+k(k>0)在x=0处取得极值,且曲线y=f(x)在点(1,f(1)))处的切线垂直于直线x+2y+1=0。
(1)求a,b的值;
(2)若函数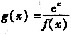
讨论g(x)的单调性。
答案
参考答案:
(1)∵f(x)=ax2+bk+k(k>0),
∴f(x)=2ax+b。
又f(x)在x=0处取得极限值,
f’(0)=b=O,
故b=0。
由曲线y=f(x)在(1,f(1)))处的切线与直线x+2y+1=0相互垂直可知该切线斜率为2,
即f’(1)=2,
有2a=2,
故a=1。
(2)由(1)知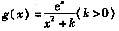
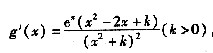
令g’(x)=0,
有x2-2x+k=0(k>0)。
①当△=4-4k<0,即当k>1时,
g’(x)>0在R上恒成立,
故函数g(x)在R上为递增函数。
②当△=4-4k=0,即当k=1时,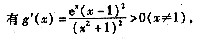
故当函数g(x)在R上为递增函数。
③当△=4-4k>0,即当0<k<1时,
方程x2-2x+k=0有两个不相等实根