问题
多选题
如图所示,两根光滑直杆(粗细可忽略不计)水平平行放置,一质量为m、半径为r的均匀细圆环套在两根直杆上,两杆之间的距离为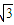 r,甲图为立体图,乙图为侧视图,现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中( ) r,甲图为立体图,乙图为侧视图,现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中( )A.每根细杆对圆环的弹力均增加 B.每根细杆对圆环的最大弹力均为mg C.每根细杆对圆环的弹力均不做功 D.每根细杆对圆环所做的功均为-  |
答案
BD
如图所示,两根光滑直杆(粗细可忽略不计)水平平行放置,一质量为m、半径为r的均匀细圆环套在两根直杆上,两杆之间的距离为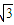 r,甲图为立体图,乙图为侧视图,现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中( ) r,甲图为立体图,乙图为侧视图,现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中( )A.每根细杆对圆环的弹力均增加 B.每根细杆对圆环的最大弹力均为mg C.每根细杆对圆环的弹力均不做功 D.每根细杆对圆环所做的功均为-  |
BD