问题
问答题
设f(x)在[a,b]上连续,a>0,在(a,b)可微.证明在(a,b)内存在ξ使
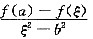
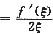 .
.
答案
参考答案:[详解] 令F(x)=x2f(a)+b2f(x)-x2f(x),则
F(a)=F(b)=b2f(a).
由罗尔定理:[*]∈(a,b)使F’(ξ)=0,
即得[*]
解析:
[分析]: 要证[*],则有2ξf(a)-2ξf(ξ)-ξ2f’(ξ)+b2f’(ξ)=0.
令F’(x)=2xf(a)-2xf(x)-x2f’(x)+b2f’(x),
得F(x)=x2f(a)+b2f(x)-x2f(x).
[评注] 关于找ξ的问题都要构造辅助函数,具体方法可参见陈文灯先生编著的《数学复习指南》.
