问题
问答题
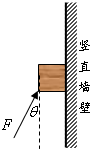
如图所示,物体的质量m=4.4kg,用与竖直方向成θ=37°的斜向右上方的推力F把该物体压在竖直墙壁上,并使它沿墙壁在竖直方向上做匀速直线运动.物体与墙壁间的动摩擦因数u=0.5,取重力加速度g=10m/s2,试分别求出物体向上和向下运动时推力F的大小.(sin37°=0.6,cos37°=0.8)
答案
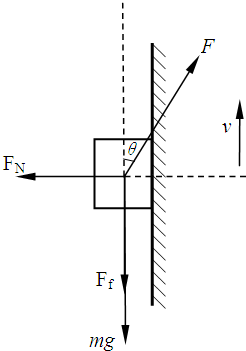
1、当物体匀速向上滑动时,受力分析如右上图所示,根据平衡条件有
水平方向:FN=Fsinθ
竖直方向:Fcosθ=Ff+mg
又因为:Ff=μFN
由以上三式可解得:
F=
=mg cosθ-μsinθ
N=88N4.4×10 0.8-0.5×0.6
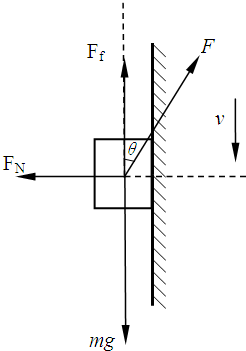
2、当物体匀速向下滑动时,受力分析如右下图所示,根据平衡条件有
水平方向:FN=Fsinθ
竖直方向:Fcosθ+Ff=mg
又因为:Ff=μFN
由以上三式可解得:
F=
=mg cosθ+μsinθ
N=40N4.4×10 0.8+0.5×0.6
答:当物体向上滑动时F=88N 当物体向下滑动时F=40N.
