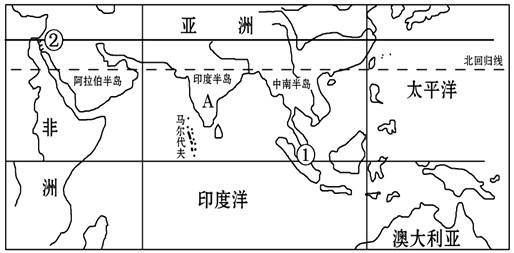
如图(a)所示,质量为M=10kg的滑块放在水平地面上,滑块上固定在一个轻细杆ABC,∠ABC=45°.在A端固定一个质量为m=2kg的小球,滑块与地面间的动摩擦因数为μ=0.5.现对滑块施加一个水平向右的推力F1=84N,使滑块做匀加速运动.求此时轻杆对小球作用力F2的大小和方向.(取g=10m/s2)有位同学是这样解的:
小球受到重力及杆的作用力F2,因为是轻杆,所以F2方向沿杆向上,受力情况如图(b)所示.根据所画的平行四边形,可以求得:
F2=
mg=2
×2×10N=202
N.2
你认为上述解法是否正确?如果不正确,请说明理由,并给出正确的解答.
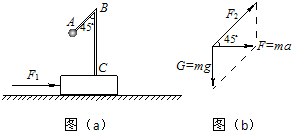
小球受重力、杆的弹力,在两个力共同作用下产生水平向右的加速度.
以小球和滑块系统为研究对象进行受力分析知
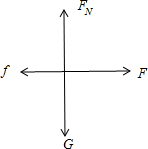
F合=F-f=F-μ(m+M)g
据牛顿第二定律知:F合=(m+M)a
系统产生的加速度a=
=F-μ(M+m)g M+m
m/s2=2m/s284-0.5×(10+2)×10 10+2
由题意知小球所受合力F合1=ma=4N
对小球进行受力分析:小球受重力、杆的弹力F,这两个力的合力大小为4N且在水平方向,
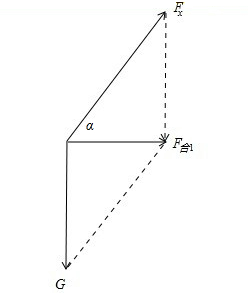
如图知:已知G=2×10N=20N,F合1=ma=4N,求Fx,则:
Fx=
=G2+F合12
N=20.4N416
Fx的方向如图所示,即所成角α的正切值为tanα=
=5G F合1
答:上述解法不正确,杆对小球的作用力不一定沿杆的方向,作用力的大小与方向具体由小球的加速度a的大小来决定,并随着a的变化而变化.
杆对小球的作用力大小为20.4N,方向斜向右上方,与水平方向夹角的正切值为5.