It was a winter morning, just a couple of weeks before Christmas 2005. While most people were warming up their cars, Trevor, my husband, had to get up early to ride his bike four kilometers away from home to work. On arrival, he parked his bike outside the back door as he usually does. After putting in 10 hours of work, he returned to find his bike gone.
The bike, a black Kona 18 speed, was our only transport. Trevor used it to get to work, putting in 60-hour weeks to support his young family. And the bike was also used to get groceries(食品杂货),saving us from having to walk long distances from where we live.
I was so sad that someone would steal our bike that I wrote to the newspaper and told them our story. Shortly after that, several people in our city offered to help. One wonderful stranger even bought a bike, then called my husband to pick it up. Once again my husband had a way to get to and from his job. It really is an honor that a complete stranger(陌生人) would go out of their way for someone they have never met before.
People say that a smile can be passed from one person to another, but acts of kindness from strangers are even more so. This experience has had a spreading effect in our lives because it made our confidence in humanity(人性)stronger as a whole. And it has also influenced us to be more mindful(在意的) of ways we can share with others. No matter how big or how small, an act of kindness shows that someone cares. And the results can be continuing for ever.
小题1:Why was the bike so important to the couple?
A.They used it for work and daily life.
B.It was borrowed from their friend.
C.It was a nice Kona18 speed.
D.The man's job was bike racing.小题2:We can learn from the text that ________.
A.the couple worked60 hours a week.
B.people were busy before Christmas
C.the stranger brought only the bike.
D.life was hard for the young family.小题3:How did people get to know the couple's problem?
A.From radio broadcasts.
B.From a newspaper.
C.From TV news.
D.From a stranger.小题4:What do the couple learn from their experience?
A.Strangers are usually of little help.
B.One should take care of their bike.
C.News reports make people famous.
D.An act of kindness can mean a lot.
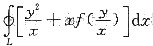 +
+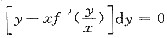 ,其中L是任一不与y轴相交的简单光滑闭曲线,试求f(x).
,其中L是任一不与y轴相交的简单光滑闭曲线,试求f(x).