问题
问答题
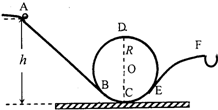
游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB,EF与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AB,EF分别与圆O相切于B、E点,C为轨道的最低点,∠BOC=37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)小球在光滑斜槽轨道AB上运动过程中加速度的大小.
(2)要使小球从A点到F点的全过程不脱离轨道,A点距离低点的竖直高度h至少多高?
答案
(1)小球沿光滑斜槽AB下滑过程,
由牛顿第二定律有:mgsin37°=ma
代入数据解得:a=gsin37°=6m/s2
(2)小球要在竖直圆轨道运动过程中不脱离轨道最高点D,速度至少为vD,则
mg=
,vD=m v 2D R gR
小球由A点到D点,由机械能守恒定律有
mgh=mg?2R+
m1 2 v 2D
由上式整理得:h=
R=0.25m5 2
答:(1)小球在光滑斜槽轨道AB上运动过程中加速度的大小为6m/s2.
(2)要使小球从A点到F点的全过程不脱离轨道,A点距离低点的竖直高度h至少0.25m.
