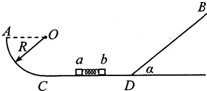
如图所示,半径为R的光滑
圆弧轨道与粗糙的斜面固定在同一竖直平面内,C、D两处与光滑水平轨道平滑连接,斜面与水平轨道的夹角为α.在水平轨道CD上,一轻质弹簧被a和b两个小物体压缩(不拴接),弹簧和小物体均处于静止状态.今同时释 放两个小物体,物体a恰好能到达圆弧轨道最高点A,物体b恰好能到达斜面最高点B,已知物体b与斜面间的动摩擦因数为μ,物体a的质量为m,物体b的质量为2m,重力加速度为g.求:1 4
(1)以CD所在的平面为重力势能的参考面,小物体滑到圆弧轨道A点时的机械能是多少?
(2)释放小球前,弹簧的弹性势能Ep;
(3)斜面高h.
(1)以水平轨道CD为参考面,小物体a滑到圆弧最高点A时的机械能为Ea=mgR①
(2)设a、b被弹开后瞬间的速度分别为νa和νb,同时释放两个小物体的过程中,两个小物体组成的系统动量守恒,有:
mva=2mvb ②
小物体a恰好到达圆弧最高点A,根据机械能守恒,有:
m1 2
=mgR ③v 2a
释放两个小物体的过程中,弹簧和两个小物体组成的系统机械能守恒,有:
EP=
m1 2
+v 2a
× 2m1 2
④v 2b
联立②③④式并解得 Ep=
mgR ⑤3 2
(3)小物体b恰好到达粗糙斜面的最高点B,根据能量守恒,有:
×2 m1 2
=μ?2mgcosα?v 2b
+ 2mgh ⑥h sinα
联立②③⑥式并解得斜面的高度为
h=
⑦Rsinα 4(sinα+μcosα)
