问题
问答题
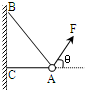
如图所示,物体A的质量为2kg,两轻绳AB和AC(LAB=2LAC)的一端连接在竖直墙上,另一端系在物体A上,今在物体A上另施加一个方向与水平方向成θ=60°角的拉力F,且保持两绳都伸直.(g取10m/s2)
(1)若使绳AB的拉力为零,则F应为多大?
(2)若使绳AC的拉力为零,则F应为多大?
答案
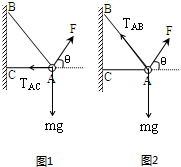
(1)(1)当使绳AB的拉力为零,小球受到重力、F和绳子CA的拉力,作出小球受力示意图如图1,则
由平衡条件得
Fsinθ=mg,得F=
=mg sinθ
N=20 3 2
N40 3 3
(2)当使绳AC的拉力为零,小球受到重力、F和绳子AB的拉力,作出小球受力示意图如图2,由几何关系得∠BAC=60°.
根据对称性可知,TAB=F,根据平衡条件
2Fsinθ=mg
解得,F=
N20 3 3
答:
(1)若使绳AB的拉力为零,则F应为
N.40 3 3
(2)若使绳AC的拉力为零,则F应为
N.20 3 3
