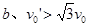如图所示,在光滑水平桌面上放有长木板 ,
, 的右端有固定挡板
的右端有固定挡板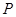 ,木板
,木板 的长度为
的长度为 。另有小物块
。另有小物块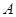 和
和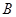 可以在长木板上滑动,
可以在长木板上滑动,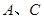 之间和
之间和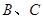 之间的动摩擦因数相同,
之间的动摩擦因数相同,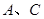 之间和
之间和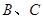 之间的最大静摩擦力等于滑动摩擦力。
之间的最大静摩擦力等于滑动摩擦力。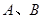 的尺寸以及
的尺寸以及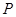 的厚度皆可忽略不计,
的厚度皆可忽略不计,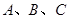 (连同挡板
(连同挡板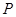 )的质量皆为
)的质量皆为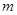 。(1)若
。(1)若 被固定在桌面上,
被固定在桌面上,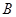 静止放在木板
静止放在木板 的中央,
的中央,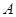 以初速度
以初速度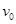 从左端冲上木板
从左端冲上木板 ,物块
,物块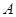 刚好能碰到
刚好能碰到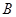 ,求
,求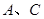 之间的动摩擦因数;(2)若
之间的动摩擦因数;(2)若 未被固定在桌面上,开始时
未被固定在桌面上,开始时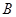 静止放在木板
静止放在木板 的中央,
的中央,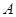 以初速度
以初速度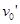 从左端冲上木板
从左端冲上木板 。a.要使物块
。a.要使物块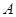 与
与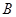 能相碰,初速度
能相碰,初速度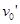 应满足的条件是什么?b.若物块
应满足的条件是什么?b.若物块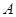 与
与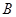 发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块
发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块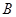 能够与挡板
能够与挡板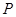 发生碰撞,初速度
发生碰撞,初速度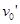 应满足的条件是什么?
应满足的条件是什么?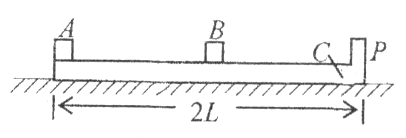
(1)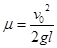 ,(2)
,(2)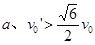 ,
,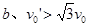
(1)C被固定住,则A在摩擦力的作用下减速运动到B点,刚好碰到B的条件是达到B点A速度为零,即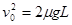 ,得
,得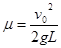
(2)a、要使物块A刚好与物块B发生碰撞,物块A运动到物块B处时,A、B的速度相等,
即v1=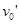 -μgt=
-μgt=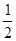 μgt ,得v1=
μgt ,得v1=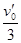
设木板C在此过程中的位移为x1,则物块A的位移为x1+L,由动能定理
-μmg(x1+L)=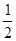 mv12-
mv12-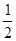 m
m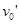 2
2
μmgx1=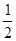 (2m)v12
(2m)v12
联立上述各式解得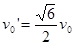 ,要使物块A、B发生相碰的条件是
,要使物块A、B发生相碰的条件是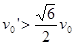
b、因为AB碰撞过程中没有机械能的损失,且两物块完全相同,所以碰撞时交换速度,就好像是A一直减速运动到挡板P一样,且刚好发生碰撞时,BC速度相等
即v2=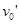 -μgt=
-μgt=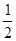 μgt ,得v2=
μgt ,得v2=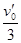
设木板C在此过程中的位移为x2,则物块AB的位移之和为x2+2L,由动能定理
-μmg(x2+2L)=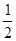 mv22-
mv22-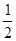 m
m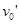 2
2
μmgx2=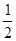 (2m)v22
(2m)v22
联立上述各式解得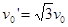 ,要使物块B与挡板发生相碰的条件是
,要使物块B与挡板发生相碰的条件是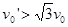
故答案为:(1)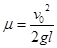 ,(2)
,(2)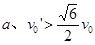 ,
,