问题
选择题
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧的形变为( )
A.伸长量为
tanθm1g k
B.压缩量为
tanθm1g k
C.伸长量为m1g ktanθ
D.压缩量为m1g ktanθ 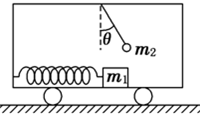
答案
对小球受力分析,如图
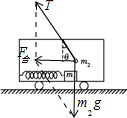
由几何关系
F合=m2gtanθ
由牛顿第二定律
a=
=gtanθF合 m
车向左加速或向右减速
对小物体受力分析,受重力、支持力和弹簧弹力,合力等于弹簧弹力,根据牛顿第二定律
F弹=m1gtanθ
物体受向左的弹力
结合胡克定律可知
弹簧的伸长量为
tanθm1g k
故选A.
