问题
计算题
如图所示，半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上，在桌面上轻
质弹簧被a、b两个小球挤压（小球与弹簧不拴接），处于静止状态。同时释放两个小球，
小球a、b与弹簧在桌面上分离后，a球从B点滑上光滑半圆环轨道最高点A时速度为
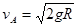。已知小球a质量为m，小球b质量为2m，重力加速度为g。求：
（1）小球a在圆环轨道最高点对轨道的压力；
（2）释放后小球b离开弹簧时的速度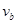
的大小；
（3）释放小球前弹簧具有的弹性势能。
答案
（1）a球对轨道的压力为mg，方向竖直向上（2）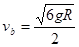
（3）
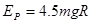
（1）设a球通过最高点时受轨道的弹力为N，由牛顿第二定律
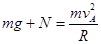① (3分)
将数据代入①式解得：N =" mg" ② （1分）
由牛顿第三定律，a球对轨道的压力为mg，方向竖直向上。 （2分）
（2）设小球a与弹簧分离时的速度大小为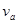
，取桌面为零势面，由机械能守恒定律得：
③（3分）
由③式解得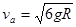 
④
小球a、b从释放到与弹簧分离过程中，总动量守恒
⑤（3分）
由⑤式解得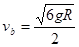： ⑥（2 分）
（3）弹簧的弹性势能为： ⑦（2分）
由⑦式解得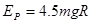： ⑧（2分）
