问题
问答题
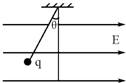
如图所示,一质量为m的带电小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线与竖直方向成θ角.
(1)判断小球带何种电荷.
(2)若已知电场强度为E、小球带电量为q,求小球的质量m.
(3)若将细线突然剪断,小球做何种性质的运动?求加速度a的大小.
答案
(1)小球受力如图,由于电场力F与场强方向相反,说明小球带负电.
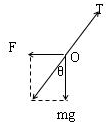
(2)小球的电场力F=qE
由平衡条件得:F=mgtanθ
则得qE=mgtanθ
解得,m=qE gtanθ
(3)剪断细线后小球做初速度为零的匀加速直线运动,
小球所受的合外力F合=mg cosθ
根据牛顿第二定律得:F合=ma
解得,a=g cosθ
答:
(1)小球带负电荷.
(2)若已知电场强度为E、小球带电量为q,小球的质量m是
.qE gtanθ
(3)若将细线突然剪断,小球做做初速度为0的匀加速直线运动,加速度a的大小为
.g cosθ
