BCD

考查知识点：本题考查的是：杠杆的平衡条件，密度知识，受力分析，浮力知识

思路分析：首先根据杠杆的平衡条件确定A、B端绳子的拉力关系，然后根据受力分析、甲物体对水平地面的压力与乙物体所受的重力大小相等判断甲乙之间的密度关系，质量关系，重力关系，最后根据浮力知识和杠杆的平衡条件判断C、D两项是否正确。

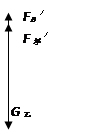
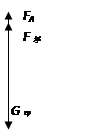
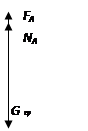
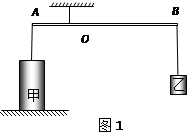
具体解答过程：一、对甲进行受力分析，如图1所示，杠杆A端的拉力大小即为绳子的拉力F_A，B端的拉力大小即为物体乙的重力（根据力的作用是相互的），利用杠杆平衡条件可得：

F_A·OA=F_B·OB，AO∶OB =1∶3，得出F_A =3F_B=3G_乙…………     ①

由对甲受力分析可列出：N_甲=G_甲 - F_A，………………②

又∵甲物体对水平地面的压力与乙物体所受的重力大小相等，即G_乙=N_甲…………③

由①③二式代入②式可得：G_乙=G_甲 - 3G_乙所以G_甲∶G_乙=4∶1故B选项是正确的。

由G_甲=m_甲g=ρ_甲V_甲g=ρ_甲S_甲h_甲g，G_乙=m_乙g=ρ_乙V_乙g=ρ_乙S_乙h_乙g

G_甲∶G_乙=4∶1 ，S_甲∶S_乙=3∶1，h_甲∶h_乙=3∶1可知ρ_甲∶ρ_乙=4∶9故A选项错误。

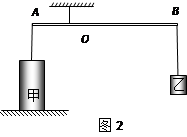
二、若将甲物体浸没于水中未触底时，保持杠杆在水平位置平衡，如图2所示，乙物体应移到距O点Ｃ处，对A进行受力分析，则根据杠杆平衡条件可知

F_A·OA=F_B·OC，OC= F_A·OA/F_B，………………④

由对甲受力分析可列出： F_A =G_甲 -  F_浮，………………⑤

G_甲∶G_乙=4∶1……………………⑥

把⑤⑥二式代入④可得OC=（４G_乙 -  F_浮）·OA/Ｇ_乙

=（４ρ_乙S_乙h_乙g- ρ_水S_甲h_甲g）·OA/ρ_乙S_乙h_乙g

再由S_甲∶S_乙=3∶1，h_甲∶h_乙=3∶1代入上式可得ＯＣ＝（4ρ_乙-9ρ_水）ＯＡ／ρ_乙，又因为ＡＢ＝L，AO∶OB =1∶3，所以ＯＡ＝L/4，故ＯＣ＝（4ρ_乙-9ρ_水）Ｌ／４ρ_乙所以Ｃ选项正确。

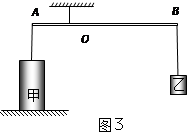
三、保持杠杆在水平位置平衡，甲、乙物体如图悬挂时与将乙物体浸没于水中未触底时，如图３所示，根据杠杆平衡条件可知F_A＇·OA=F_B＇·OB，…………………………⑦

对甲、乙进行受力分析如图３，则F_A＇=G_甲 - 　N_甲＇………………………………⑧

F_Ｂ＇ =G_乙 -  F_浮＇………………………………………………………………⑨

把⑥⑧⑨代入⑦可得（４G_乙 - 　N_甲＇）·ＯＡ＝（G_乙 -  F_浮＇）ＯＢ

有F_浮＇＝ρ_水S_乙h_乙g，3OA=OB，G_乙=ρ_乙S_乙h_乙g，N_甲＇＝ρ_乙S_乙h_乙g＋３ρ_水S_乙h_乙g

由题意杆在水平位置平衡时，甲物体对水平地面的压力与乙物体所受的重力大小相等可知

N_甲＝G_乙＝ρ_乙S_乙h_乙g，所以N_甲∶N_甲´=ρ_乙∶（ρ_乙+3ρ_水）故选项Ｄ正确。

所以此题的答案为ＢＣＤ。

试题点评：这道题是力学部分的综合题，结合了杠杆的平衡条件、密度知识、受力分析、浮力知识的综合应用，所以比较难。