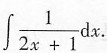如图,一根绝缘细杆固定在磁感应强度为B的水平匀强磁场中,杆和磁场垂直,与水平方向成θ角.杆上套一个质量为m、电量为+q的小球.小球与杆之间的动摩擦因数为μ.从A点开始由静止释放小球,使小球沿杆向下运动.设磁场区域很大,杆很长.已知重力加速度为g.求:
(1)定性分析小球运动的加速度和速度的变化情况;
(2)小球在运动过程中最大加速度的大小;
(3)小球在运动过程中最大速度的大小.
(1)由于洛伦兹力作用下,导致压力减小,则滑动摩擦力也减小,所以加速度增加,当洛伦兹力大于重力的垂直于杆的分力时,导致滑动摩擦力增大,从而出现加速度减小,直到处于受力平衡,达到匀速直线运动.
因此小球先做加速度增大的加速运动,再做加速度减小的加速运动,最后做匀速直线运动.
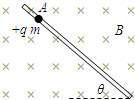
(2)当杆对小球的弹力为零时,小球加速度最大.
小球受力如图1所示
根据牛顿第二定律 mgsinθ=ma
解得:a=gsinθ
(3)当小球所受合力为零时,速度最大,设最大速度为vm
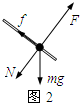
小球受力如图2所示
根据平衡条件 qvmB=N+mgcosθ
mgsinθ=f
滑动摩擦力 f=μN
解得:vm=mg(sinθ+μcosθ) μBq
答:(1)先做加速度增大的加速运动,再做加速度减小的加速运动,最后做匀速直线运动;
(2)小球在运动过程中最大加速度的大小gsinθ;
(3)小球在运动过程中最大速度的大小为 vm=
.mg(sinθ+μcosθ) μBq