如图10所示,光滑水平面上有一长板车,车的上表面OA段是一长为L的水平粗糙轨道,A的右侧光滑,水平轨道左侧是一光滑斜面轨道,斜面轨道与水平轨道在O点平滑连接.车右端固定一个处于锁定状态的压缩轻弹簧,其弹性势能为Ep,一质量为m的小物体(可视为质点)紧靠弹簧,小物体与粗糙水平轨道间的动摩擦因数为μ,整个装置处于静止状态.现将轻弹簧解除锁定,小物体被弹出后滑上水平粗糙轨道.车的质量为 2m,斜面轨道的长度足够长,忽略小物体运动经过O点处产生的机械能损失,不计空气阻力.求:
(1)解除锁定结束后小物体获得的最大动能;
(2)当μ满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最大高度为多少?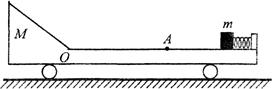
(1)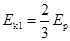 (2)
(2)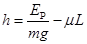
本题考查系统动量守恒,根据系统受力情况分析出在解锁弹开后动量守恒,因为小车表面粗糙系统的机械能不守恒
(1)、设解锁弹开后小物体的最大速度饷大小为v1,小物体的最大动啦为Ek ,此时长板车的速度大小为v2,研究解锁弹开过程小物体和车组成的系统,根据动量守恒和机械能守恒,
有 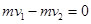 ① (2分)
① (2分)
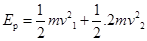 ② (2分)
② (2分)
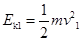 ③(2分)
③(2分)
联立①②③式解得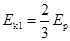 .(2分)
.(2分)
(2)、小物体相对车静止时,二者有共同的速度设为v共,
长板车和小物体组成的系统水平方向动量守恒 :
 ④ (2分)
④ (2分)
所以v共=0
要使小物体能滑上斜面轨道,必须满足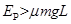 (2分)
(2分)
即当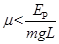 时,小物体能滑上斜面轨道
时,小物体能滑上斜面轨道
设小物体上升的最大高度为h,此瞬间小物体相对车静止,由④式知两者有共同速度为零.
根据系统能量守恒有 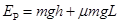 (2分)
(2分)
解得: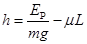 .(2分)
.(2分)