问题
问答题
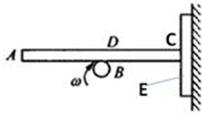
如图所示,重为G的均匀木棒AC水平地搁在一个圆柱体B上,二者的接触点为D,且AD:DC=17:15.当圆柱体绕着固定中心顺时针方向转动时,与棒的右端C紧靠着的木板E恰能沿光滑竖直墙面匀速下滑.若木棒与圆柱体之间、木棒与木板之间的动摩擦因数相同,试求:
(1)木板E的重力为多大?
(2)圆柱体B对木棒AC的支持力为多大?
(3)动摩擦因数为多大?
答案
(1)设木棒的重心位置在棒的O点,木棒与木板间的摩擦力大小为f2,则对木棒,根据力矩平衡得
G?OD=f2?DC
得 f2=G?
=OD DC
G1 15
木板E沿光滑竖直墙面匀速下滑,则有 木板E的重力GE=f2=
G1 15
(2)根据木棒受力衡得,
竖直方向:圆柱体B对木棒AC的支持力N1=G+f2=
G.16 15
(3)设木棒与圆柱体间的摩擦力大小为f1,木棒与木板间的弹力大小为N2,
则 f1=μN1=N2,
又GE=f2=
G,N1=1 15
G,代入解得,μ=0.2516 15
答:
(1)木板E的重力为
G.1 15
(2)圆柱体B对木棒AC的支持力为
G.16 15
(3)动摩擦因数为0.25.
