如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点.A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧处于原长状态时,物块恰能与固定在墙上的L形挡板接触于B处但无挤压.现使一质量为m的小球从圆弧轨道上距水平轨道高h处的D点由静止开始下滑.小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连.(整个过程中,弹簧没有超过弹性限度.不计空气阻力,重力加速度为g)
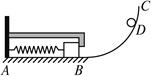
(1)试求弹簧获得的最大弹性势能;
(2)求小球与物块第一次碰后沿BC上升的最大高度;
(3)若R>>h,每次从小球接触物块至物块撞击L形挡板历时均为Δt,则小球由D点出发经多长时间第三次通过B点?
(1)
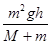(2)
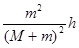(3)
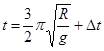
解:(1)由小球运动至第一次碰前,据动能定理有:
mgh=mv02/2 ① (1分)
对碰撞过程,据动量守恒:
mv0=(M+m)v1 ② (1分)
碰后压缩弹簧过程中,M、m及弹簧系统机械能守恒:
Epm=(M+m)v12/2 ③ (1分)
由①②③式联立解得:
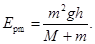④ (2分)
(2)第一次碰后小球向BC轨道运动的初速度即为v1,由机械能守恒得:
⑤ (1分)
由①②⑤式联立解得: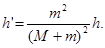
⑥ (2分)
(3)小球在BC段运动可等效为单摆,其周期为:
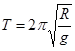⑦ (1分)
分析得小球第三次通过B点历时为:
⑧ (2分)
由⑦⑧式联立解得:
⑨ (2分)