问题
计算题
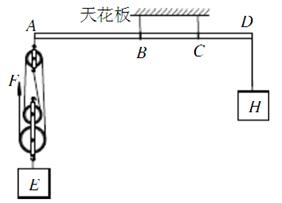
如图所示，轻质杠杆AD用两根软绳悬挂于天花板上，两绳分别系在杠杆上的B、C两点。已知杠杆的长度为0.8m，BC间的距离为0.2m，CD间的距离为0.2m。用细绳将滑轮组固定在杠杆的A端，物体E（其质量可变）挂在动滑轮的挂钩上，每个滑轮重均为60N。物体H通过细绳挂在杠杆的D端，其质量始终保持不变。为使杠杆AD保持水平平衡，滑轮组所能提升重物E的最大质量m1与最小质量m2之比为4:1。杠杆、细绳的质量及一切摩擦均可忽略不计，取g= 10N/kg。求：
（1）滑轮组对杠杆A端的最大拉力FA1与最小拉力FA2之比；
（2）重物E的最大质量m1；
（3）滑轮组的最小机械效率。（百分号前保留整数）
答案
(1)FA1:FA2=3:1 (2) m1 =160kg (3)77%
题目分析：（1）以B点为支点时，滑轮组对杠杆A端有最大拉力FA1；以C点为支点时，滑轮组对杠杆A端有最小拉力FA2。
由图中距离关系可知：AB=0.4m，AC=0.6m，BD=0.4m
根据杠杆平衡条件：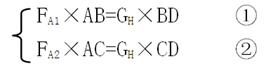
1分
①/②得出：FA1:FA2=3:1 1分
（2）以定滑轮为研究对象，受力分析如图甲、乙所示；以两个动滑轮和物体E整体为研究对象，受力分析如图丙、丁所示。 1分
得出如下平衡方程：
1分
因为m1:m2=4:1，所以G1:G2=m1:m2=4:1
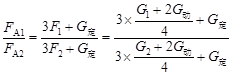
代入数据：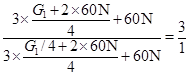
，解得：G1=1600N
m1=G1/g=160kg 1分
（3）因为G1:G2= 4:1，所以G2= G1/ 4=1600N/4=400N
2分