问题
计算题
（10分）如图所示，木板B的质量M="2" kg，与右墙距离为S．物体A（可视为质点）质量m="l" kg，以初速度v0="6" m/s从左端水平滑上B．己知A与B间的动摩擦因数μ=0.2，在B第一次撞墙前，A已经与B相对静止．地面光滑，B与两面墙的碰撞都是弹性的。求：
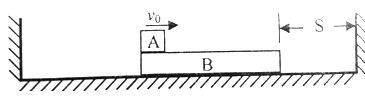
①S的最小值：
②若A始终未滑离B，A相对于B滑行的总路程是多少？
答案
2m 9m
①设B与挡板相碰时的速度大小为v1，
由动量守恒定律得mv0=（M+m）v1，（2分）
求出v1=2m/s. （1分）
A与B刚好共速时B到达挡板S距离最短，对B用动能定理，
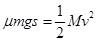（2分）
S的最小值为s= 2m（1分）
②经过足够多次的碰撞后，由于不断有摩擦力做功，最终AB速度都变为零，则在整个过程中，平板车和物块的动能都克服摩擦力做功转化为内能，因此有:
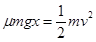（3分）
x=9m （1分）