问题
单项选择题
设矩阵
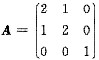，矩阵B满足ABA*=2BA*+E，其中A*为A的伴随矩阵，E是单位矩阵，则|B|=( )．
答案
参考答案：A
解析：
方法一 利用伴随矩阵的性质及矩阵乘积的行列式性质求行列式的值．
ABA*=2BA*+E
ABA*-2BA*=E．
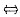(A-2E)BA*=E，
所以|A-2E||B||A*|=|E|=1，
．选(A)．
方法二 由A*=|A|A-1，得
ABA*=2BA*+E
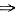AB|A|A-1=2B|A|A-1+AA-1
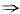|A|AB=2|A|B+A
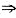|A|(A-2E)B=A
|A|3|A-2E||B|=|A| 所以