问题
问答题
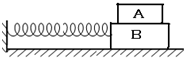
如图所示,A、B质量分别为m和M,B系在固定于墙上的水平轻弹簧的另一端,并置于光滑的水平面上,弹簧的劲度系数为k,将B向右拉离平衡位置x后,无初速度释放,在以后的运动中A、B保持相对静止,求
(1)A在运动中受到的摩擦力最大值为多少.
(2)在从开始到运动
周期的过程中,摩擦力对A受做功为多少?(提示:对均匀变化的力求平均力可以应用:1 4
=. F
)F1+F2 2
答案
(1)当刚释放时,以整体为研究对象,根据牛顿第二定律得:kx=(M+m)a
此时AB加速度最大为:am=kx m+M
此时A受摩擦力最大,根据牛顿第二定律得:
fm=mam=mkx M+m
故A在运动中受到的摩擦力最大值为:fm=
.mkx M+m
(2)在
周期时间内,A受,摩擦力线性减小到零,所以根据1 4
=. F
可知A受到的摩擦力平均值为:F1+F2 2
f=
=fm 2 mkx 2(M+m)
则摩擦力对A做的功:
W=f*x=mkx 2(M+m)
故在从开始到运动
周期的过程中,摩擦力对A受做功大小为:W=1 4
.mkx 2(M+m)
