问题
问答题
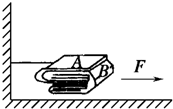
如图所示,有两本完全相同的书A、B,书重均为5N,若将两本书等分成若干份后交叉地叠放在一起置于光滑桌面上,并将书A固定不动,用水平向右的力F把书B匀速抽出,现测得一组数据如下:
| 实验次数 | 1 | 2 | 3 | 4 | … | n |
| 将书分成的份数 | 2 | 4 | 8 | 16 | … | 逐页交叉 |
| 力F的大小(N) | 4.5 | 10.5 | 22.5 | 46.5 | … | 190.5 |
(1)若将书分成32份,力F应为多大?
(2)该书的页数.
(3)该书任意两张纸之间的动摩擦因数为多少?
答案
(1)对表中数据分析可知:将书分成四份时,力F比前一次增加6 N,将书分成8份时,力F比前一次增加12 N,由此可知,每这样分一次,增加的力是上次增加的力的2倍,
故将书分成32份,力F应比前一次增加48 N.
故F=46.5N+48 N=94.5 N,
所以将书分成32份,力F应为94.5 N.
(2)将书分成64份时,比分成32份时力F应增大96N,故94.5N+96N=190.5 N,可知书的总页数应为128页
(3)以分成2份为例,对书B列方程有:
F=
μ?mg+μ?mg+1 2
μ?mg=3μG3 2
因为G=5 N,所以μ=0.3
答:(1)若将书分成32份,力F应为94.5N;
(2)该书的页数为128页;
(3)本书任意两张纸之间的滑动摩擦系数μ为0.3.
