问题
计算题
如图所示，小车A静止在光滑水平面上，半径为R的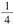
_光滑圆弧轨道固定在小车上，光滑圆弧下端部分水平，圆弧轨道和小车的总质量为M0质量为m的小滑块B以水平初速度V0滑上小车，滑块能从圆弧上端滑出。求：
①小滑块刚离开圆弧轨道时小车的速度大小；
②小滑块到达最高点时距圆弧轨道上端的距离。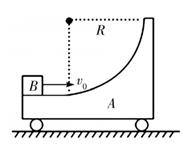
答案
①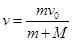
②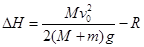
①以小滑块和小车（含光滑圆弧轨道）为研究对象，水平方向动量守恒，当小滑块从圆弧轨道上端滑出后，小滑块的水平速度与小车速度相同，则有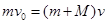 
（2分）
故小车的速度大小为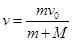 （1分）
②小滑块到达最高点时的速度与小车速度相同，由①并结合机械能守恒定律有
（2分）
小滑块距光滑圆弧轨道上端的距离为
（2分）
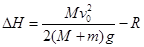联立解得 （2分）
本题考查了动量守恒和功能关系，小车和滑块组成的系统动量守恒，可得小车的速度，当小滑块到达最高点时的速度与小车速度相同，并结合机械能守恒定律可得
从而算出距离