(18分)图18(a)所示的装置中,小物块A、B质量均为m,水平面上PQ段长为l,与物块间的动摩擦因数为μ,其余段光滑。初始时,挡板上的轻质弹簧处于原长;长为r的连杆位于图中虚线位置;A紧靠滑杆(A、B间距大于2r)。随后,连杆以角速度ω匀速转动,带动滑杆作水平运动,滑杆的速度-时间图像如图18(b)所示。A在滑杆推动下运动,并在脱离滑杆后与静止的B发生完全非弹性碰撞。
 (1)求A脱离滑杆时的速度uo,及A与B碰撞过程的机械能损失ΔE。
(1)求A脱离滑杆时的速度uo,及A与B碰撞过程的机械能损失ΔE。
(2)如果AB不能与弹簧相碰,设AB从P点到运动停止所用的时间为t1,求ω得取值范围,及t1与ω的关系式。
(3)如果AB能与弹簧相碰,但不能返回道P点左侧,设每次压缩弹簧过程中弹簧的最大弹性势能为Ep,求ω的取值范围,及Ep与ω的关系式(弹簧始终在弹性限度内)。
(1)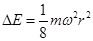 (2)
(2)
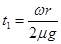 (3)
(3)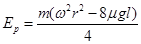
(1)由题知,A脱离滑杆时的速度uo=ωr
设A、B碰后的速度为v1,由动量守恒定律
m uo="2m" v1
A与B碰撞过程损失的机械能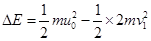
解得 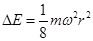
(2)AB不能与弹簧相碰,设AB在PQ上运动的加速度大小为a,由牛顿第二定律及运动学规律
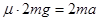 v1=at1
v1=at1 
由题知
联立解得
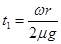
(3)AB能与弹簧相碰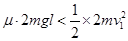
不能返回道P点左侧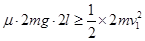
解得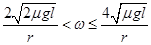
AB在的Q点速度为v2,AB碰后到达Q点过程,由动能定理
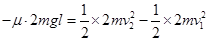
AB与弹簧接触到压缩最短过程,由能量守恒
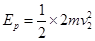
解得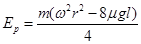 。
。
