如图所示，一根均质绳质量为M，其两端固定在天花板上的A、B两点_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题选择题

如图所示，一根均质绳质量为M，其两端固定在天花板上的A、B两点，在绳的中点悬挂一重物，质量为m，悬挂重物的绳PQ质量不计．设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角，则

tanα

tanβ

等于（　　）

A．

m

M+m

B．

m+M

5m

C．

m

M

D．

m

2m+M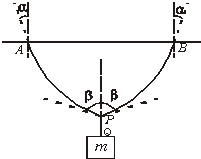

答案

设绳子端点处和中点处绳子张力分别为F₁、F₂．

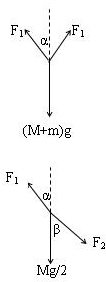
对整体研究，根据平衡条件得

F₁cosα=

1

2

(M+m)g ①

对左半边绳子研究得

F₁cosα=F₂cosβ+

1

2

Mg ②

F₁sinα=F₂sinβ ③

由①②得到 F₂cosβ=

1

2

mg ④

则由③：①得 tanα=

2F2sinβ

(M+m)g

⑤

由③：④得 tanβ=

2F1sinα

mg

⑥

所以由③⑤⑥联立得

tanα

tanβ

=

m

M+m

故选A

单项选择题共用题干题

患儿2岁半，病初2天有轻微咳嗽，随后出现高热，体温达40℃，烦躁，频繁呕吐，查体：神志清楚，颈项强直，脑膜刺激征阳性，巴宾斯基征阳性；脑脊液检查外观混浊，压力增高，白细胞计数2×10¹⁰/L，以多核细胞为主，糖2.2mmol/L，蛋白质1100mg/L。

入院后患儿出现撞头、尖叫、烦躁不安，呕吐加重，此对应立即给予（）

A.20%的甘露醇0.25～0.5g/kg快速静滴

B.硬脑膜下穿刺

C.大量抗生素静滴

D.退热处理

E.镇静

填空题

编报WW（中等强度）电码52、53、72、73、86时，其有效能见度一般介于（）。